1　はじめに

こんにちは，どこでもかんたんVR「スペースリー」の研究開発チームのhasegawaです。2020年8月でちょうど入社して1年になりました。業務としては画像処理まわりを担当しており，機械学習やその他の一般的な画像処理アルゴリズムの双方を使いながら，将来の新機能開発に繋がるアルゴリズムの開発を行なっています。今回は業務の中で必要となった前処理的な部分について解説します。

360度画像の表現として，一般的にはパノラマ画像や魚眼画像が用いられることが多いのですが，それぞれの表現にメリット・デメリットがあるため，画像処理などを行う際には目的に応じて2つの表現を相互に変換する機会が多々あります。また，機械学習の分野でも360度パノラマ画像を用いた3Dモデル生成アルゴリズムなどの提案がされています[1][2]。しかし，パノラマ画像は歪みをもっており最終的な生成モデルのクオリティが低下するため，傾きの補正や魚眼画像・透視図への射影変換などの前処理が必要な場合があります。

最近ではパノラマ写真を畳み込む際に，透視図に射影変換した場合と等価になるようなカーネルを用いた手法も提案されています[3][4]。

透視図への射影と魚眼画像への射影を比べると，圧倒的に透視図への射影の方が使用頻度が高いのですが，その分ネットで公開されている情報も多いので今回の記事ではあえて魚眼画像への射影について説明します。

パノラマ画像と魚眼画像の射影変換は3次元の極座標の図が書ければすぐ求められますが，3次元でイメージしたり，実装までやってみると結構手間が掛かります。

今回はスペースリーにおける画像処理の前処理的な部分の取組みとして，360度パノラマ写真から2つの180度魚眼画像（いわゆるDual Fisheye Image）に変換する過程を紹介します。

2　魚眼画像とパノラマ画像

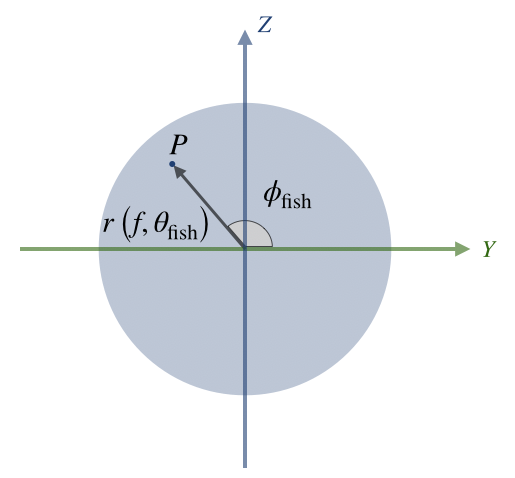
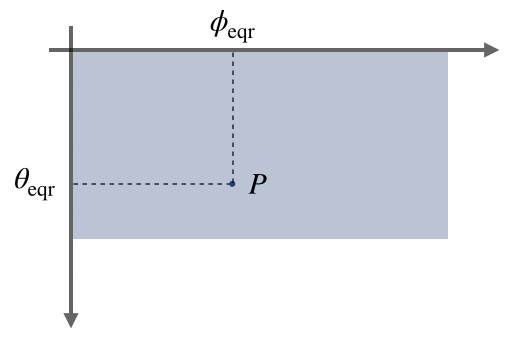
1枚の魚眼画像は下図のように2次元極座標で表現され，パノラマ写真は緯度・経度の2次元直交座標で表現されます。


パノラマ2次元直交座標	魚眼2次元極座標

この2つの表現のダイレクトな変換を脳内で考えれられればいいですが，式がかなり複雑になり困難なので，間に3次元直交座標を考えます。

2.1　魚眼座標と3次元直交座標

先ほど示した魚眼2次元極座標と一致するように変数をおいた3次元極座標の図を以下に示します。

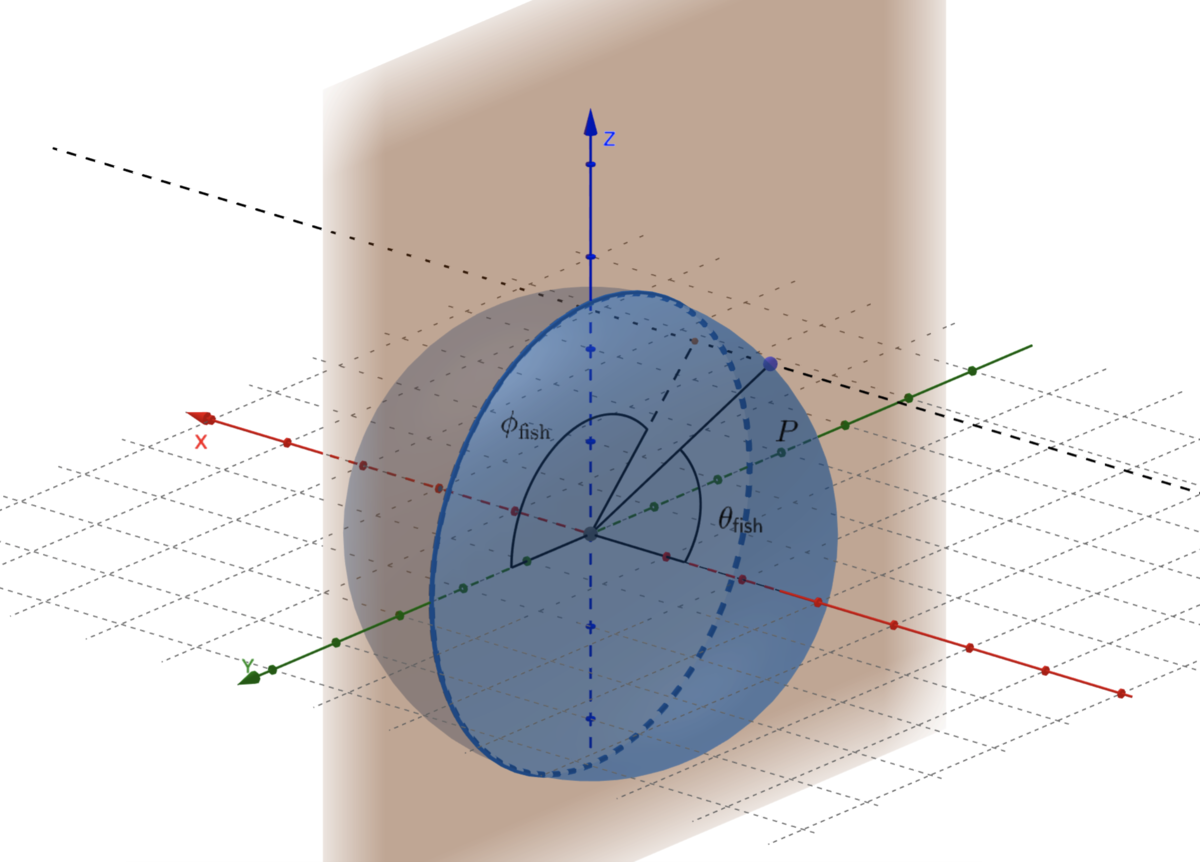
魚眼座標と3次元直交座標

3次元空間では中央にレンズの中心があり球面は外部の情景を投影したスクリーンになっているような状況です。 $\phi_\mathrm{fish}$がスクリーン上の点$P$と$Y$軸がなす角であり，$\theta_\mathrm{fish}$がスクリーン上の点$P$と$X$軸がなす角です。この時，レンズからスクリーンまでの距離（球面の半径）がレンズの焦点距離$f$になっています。魚眼画像1枚では全体の半分しか写せないですが，今は図中の$X<0$の範囲について説明します。反対側は符号とかが変わるだけです。

魚眼画像における点$P$までの半径$r$は，角度$\theta_\mathrm{fish}$と焦点距離$f$の値によって決められます。どのような式になるかは射影方式によって異なるのですが，魚眼の写真で一般的に用いられる等距離射影方式では以下のような式で表されます[5]。 $$ r = f \theta_\mathrm{fish} \tag{1} $$

点$P$の3次元直交座標における座標$(X, Y, Z)$を魚眼座標のパラメータなどを用いて表すと以下のようになります。

$$ \begin{align} \begin{split} X &= - f \cos{\theta_\mathrm{fish} } \\ Y &= f\sin{\theta_\mathrm{fish} } \cos{\phi_\mathrm{fish}}\\ Z &= f\sin{\theta_\mathrm{fish} } \sin{\phi_\mathrm{fish} }\\ \end{split} \tag{2} \end{align} $$

魚眼画像と3次元直交座標の関係を表すことができたので，次はパノラマ写真と3次元直交座標の関係を説明します。

2.2　パノラマ座標と3次元直交座標

パノラマ2次元直交座標と一致するように変数をおいた3次元極座標の図を以下に示します。

魚眼座標と3次元直交座標

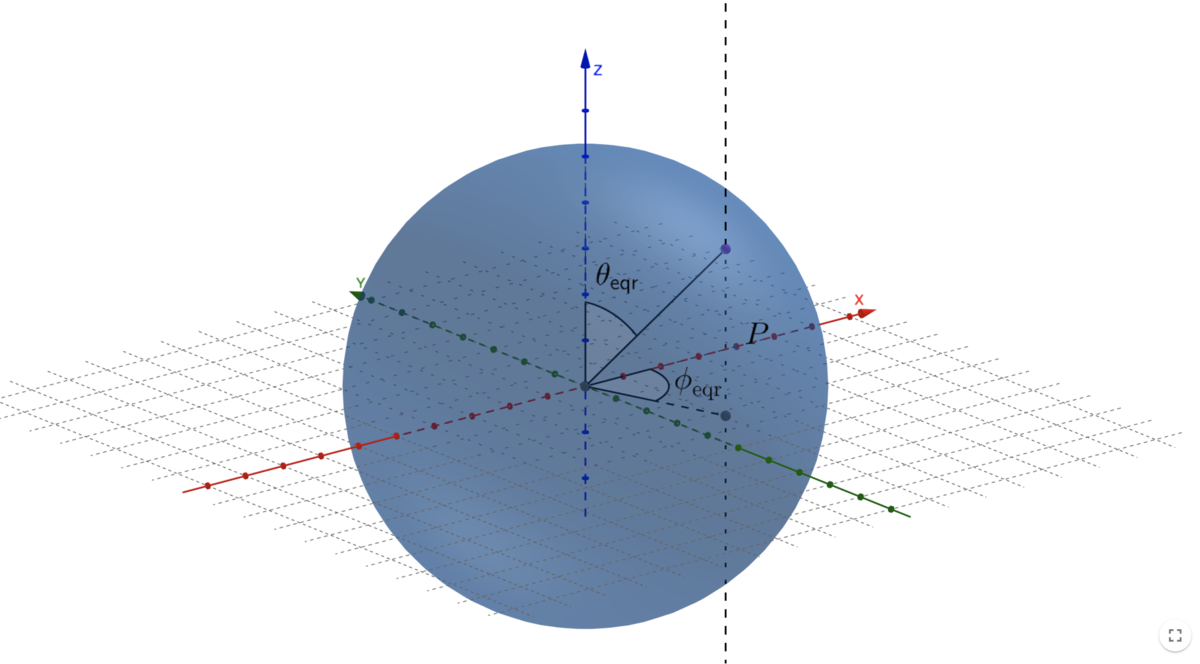
パノラマ写真では一般的に正距円筒図法（equirectangular）が用いられます。

こちらも先ほどと同様に点$P$の座標をパノラマ2次元直交座標のパラメータで表現すると以下のようになります。

$$ \begin{align} \begin{split} X &= f\sin{\theta_\mathrm{eqr} } \cos{\left( - \phi_\mathrm{eqr} \right)}\\ Y &= f\sin{\theta_\mathrm{eqr} } \sin{\left( - \phi_\mathrm{eqr} \right)}\\ Z &= f \cos{\theta_\mathrm{eqr} } \\ \end{split} \tag{3} \end{align} $$

パノラマ画像と3次元直交座標の関係を表すことができたので，あとは3次元直交座標を中継して魚眼画像とパノラマ写真の関係式を導けば良いです。

3　パノラマ画像から魚眼画像への変換

3.1　パノラマ座標と魚眼座標の関係式

ここまでで得られた式から，点$P$の座標に関して以下の等式が成立します。

$$ \begin{align} \begin{split} & f\sin{\theta_\mathrm{eqr} } \cos{\left( - \phi_\mathrm{eqr} \right)} = - f \cos{\theta_\mathrm{fish} } \\ &f\sin{\theta_\mathrm{eqr} } \sin{\left( - \phi_\mathrm{eqr} \right)} = f\sin{\theta_\mathrm{fish} } \cos{\phi_\mathrm{fish} }\\ &f \cos{\theta_\mathrm{eqr} } = f\sin{\theta_\mathrm{fish} } \sin{\phi_\mathrm{fish} }\\ \end{split} \tag{4} \end{align} $$

これを変形すると，

$$ \begin{align} \begin{split} &\theta_\mathrm{fish} = \mathrm{arc}\cos{ \left( - \sin\theta_\mathrm{eqr} \cos\phi_\mathrm{eqr} \right)}\\ &\phi_\mathrm{fish} = \mathrm{arc}\tan2{\left(\cos\theta_\mathrm{eqr}, - \sin\theta_\mathrm{eqr} \sin\phi_\mathrm{eqr} \right)} \end{split} \tag{5} \end{align} $$

以上の結果から，パノラマ画像のパラメータから魚眼画像の座標が得られるようになりました（逆もまた然り）。

3.2　実装上で必要な変換式

ここで終わっても良いですが，変換コードを実装する際には画像はColumnとRowの座標で表現されるため，このままでは困ります。以降，ColumnとRowの座標を記事中ではCR座標と呼びます。

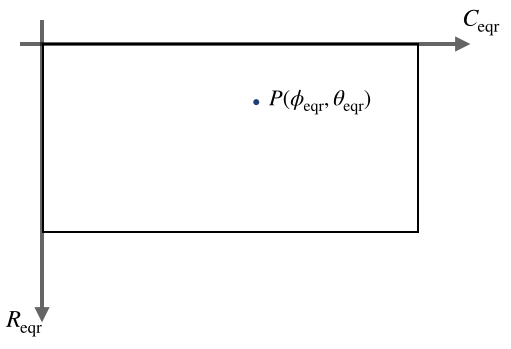
例えば以下のように対応するパノラマ画像と魚眼画像の変換を考えます。


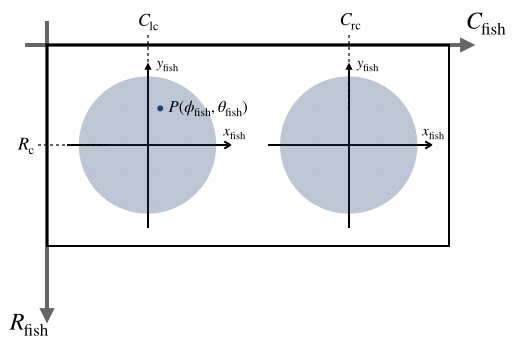パノラマ画像	魚眼2次元画像

順番に必要な関係式を列挙していきます。

3.2.1　パノラマ画像におけるCR座標への変換式

$C_\mathrm{eqr}$と$\phi_\mathrm{eqr}$，$R_\mathrm{eqr}$と$\theta_\mathrm{eqr}$はそれぞれ比例するので，適当に係数を書ければ変換ができますが，以下のように分子にある係数を焦点距離$f$の値にしました。

$$ \begin{align} \begin{split} \phi_\mathrm{eqr} &= \frac{C_\mathrm{eqr}}{f}\\ \theta_\mathrm{eqr} &= \frac{R_\mathrm{eqr}}{f} \\ \end{split} \tag{6} \end{align} $$

これは解像度の低下を避けるためで，パノラマ画像の横幅（$f\cdot 2\pi$）が投影元の3次元球面の大円の円周（$2f\cdot \pi$）に一致し，縦幅（$f\cdot \pi$）が大円の円周のちょうど半分になるようにしています。こうすることで，パノラマ写真の全てのColumnとRowにおいて，投影元の3次元球面のスクリーンのColumnとRowのピクセル数を下回ることがないため，解像度の低下が起こりません。

3.2.2　魚眼画像における極座標からそれぞれのxy座標への変換式

変換先の魚眼画像では180度の魚眼画像が2つ並ぶので，それぞれの魚眼に対してxy座標への変換を行います。

$$ \begin{align} \begin{split} x_\mathrm{fish} &= \begin{cases} r \cos{\phi_\mathrm{fish} } & \mathrm{(Left)} \\ - r \cos{\phi_\mathrm{fish} } & \mathrm{(Right)} \end{cases}\\ &= \begin{cases} f \theta_\mathrm{fish} \cos{\phi_\mathrm{fish} } & \mathrm{(Left)} \\ - f \theta_\mathrm{fish} \cos{\phi_\mathrm{fish} } & \mathrm{(Right)} \end{cases}\\ y_\mathrm{fish} &= r \sin{\phi_\mathrm{fish} } \\ &= f \theta_\mathrm{fish} \sin{\phi_\mathrm{fish} }
\end{split} \tag{7} \end{align} $$

3.2.3　魚眼画像におけるそれぞれのxy座標からCR座標への変換式

$$ \begin{align} \begin{split} C_\mathrm{fish} &= \begin{cases} C_{lc} + x_\mathrm{fish} & \mathrm{(Left)} \\ C_{rc} + x_\mathrm{fish} & \mathrm{(Right)} \\ \end{cases} \\ R_\mathrm{fish} &= R_{c} -y_\mathrm{fish} \\ \end{split} \tag{8} \end{align} $$

ここまでで得られた変換式を (6)(5)(7)(8)の順に使うと，$\left( C_\mathrm{eqr}, R_\mathrm{eqr} \right)$から$\left( C_\mathrm{fish}, R_\mathrm{fish} \right)$への変換が完了します。

4　PythonとOpenCVによるサンプルコード

下のコードははOpenCVのremap関数を用いて実装した例です。 remap関数では引数として逆変換のmapを渡すので，先ほど計算と反対に(8)(7)(5)(6)の順に実装しています。

from pathlib import Path
import cv2
import numpy as np


def eqr2dualfisheye(eqr_image_path, rad_limit=True):

    eqr_image = cv2.imread(str(eqr_image_path))
    eqr_img_h, eqr_img_w = eqr_image.shape[:2]

    f = eqr_img_h / np.pi  # focal length

    # RICHOの360度カメラ THETA Vのサイズ比に合わせてみた
    THETA_V_fisheye_img_h, THETA_V_fisheye_img_w = (2896, 5792)
    THETA_V_eqr_img_h, THETA_V_eqr_img_w = (2688, 5376)

    fisheye_img_h = -(- eqr_img_h * THETA_V_fisheye_img_h // THETA_V_eqr_img_h)
    fisheye_img_w = -(- eqr_img_w * THETA_V_fisheye_img_w // THETA_V_eqr_img_w)

    c_fisheye_lc = fisheye_img_w // 4        # 左側魚眼の中心のColumn座標
    c_fisheye_rc = fisheye_img_w // 4 * 3    # 右側魚眼の中心のColumn座標
    c_fisheye_border = fisheye_img_w // 2    # 左右魚眼の境界
    r_fisheye_c = fisheye_img_h // 2         # 左右魚眼の中心のRow座標

    c_fisheye_map, r_fisheye_map = np.meshgrid(range(fisheye_img_w), range(fisheye_img_h))

    # 魚眼CR座標 -> 魚眼xy座標
    y_fisheye_map = fisheye_img_h - r_fisheye_map - r_fisheye_c
    x_fisheye_map = np.zeros((fisheye_img_h, fisheye_img_w))
    x_fisheye_map[:, :c_fisheye_border] = c_fisheye_map[:, :c_fisheye_border] - c_fisheye_lc
    x_fisheye_map[:, c_fisheye_border:] = c_fisheye_map[:, c_fisheye_border:] - c_fisheye_rc

    # 魚眼xy座標 -> 魚眼極座標
    phi_fisheye_map = np.zeros((fisheye_img_h, fisheye_img_w))
    phi_fisheye_map[:, :c_fisheye_border] = np.arctan2(y_fisheye_map[:, :c_fisheye_border], x_fisheye_map[:,:c_fisheye_border])
    phi_fisheye_map[:, c_fisheye_border:] = np.arctan2(y_fisheye_map[:, c_fisheye_border:], - x_fisheye_map[:,c_fisheye_border:])
    phi_fisheye_map = phi_fisheye_map % (2 * np.pi)
    theta_fisheye_map = np.sqrt(x_fisheye_map**2 + y_fisheye_map**2) / f
    theta_fisheye_map[:, c_fisheye_border:] = np.pi - theta_fisheye_map[:, c_fisheye_border:]

    # 魚眼極座標 -> パノラマ緯度経度座標 -> パノラマCR座標
    c_eqr_map = f * (np.arctan2(-np.sin(theta_fisheye_map) * np.cos(phi_fisheye_map), -np.cos(theta_fisheye_map)) % (2 * np.pi))
    r_eqr_map = f * np.arccos(np.sin(theta_fisheye_map) * np.sin(phi_fisheye_map))

    # 魚眼CR座標 -> パノラマCR座標の完成
    fisheye2eqr_map_c = c_eqr_map.astype('float32')
    fisheye2eqr_map_r = r_eqr_map.astype('float32')

    dual_fisheye_image = cv2.remap(eqr_image, fisheye2eqr_map_c, fisheye2eqr_map_r, cv2.INTER_CUBIC, borderMode=cv2.BORDER_WRAP)

    return dual_fisheye_image